
2024 लेखक: Lynn Donovan | [email protected]. अंतिम बार संशोधित: 2023-12-15 23:47
कंप्यूटर विज्ञान में, प्राइम का (जर्निक के रूप में भी जाना जाता है) कलन विधि एक लालची है कलन विधि जो एक भारित अप्रत्यक्ष ग्राफ के लिए न्यूनतम फैले हुए पेड़ को ढूंढता है। इसका मतलब है कि यह किनारों का एक सबसेट ढूंढता है जो एक पेड़ बनाता है जिसमें प्रत्येक शीर्ष शामिल होता है, जहां पेड़ में सभी किनारों का कुल वजन कम होता है।
इस संबंध में, प्रिम्स क्रुस्कल से बेहतर क्यों है?
क्रुस्कल का एल्गोरिथम: करता है बेहतर विशिष्ट स्थितियों में (विरल रेखांकन) क्योंकि यह सरल डेटा संरचनाओं का उपयोग करता है। प्राइम का एल्गोरिथम: सीमा में काफी तेज है जब आपके पास कई और किनारों के साथ वास्तव में घना ग्राफ है से कोने।
क्या प्राइम का एल्गोरिदम इष्टतम है? प्राइम का एल्गोरिदम एक लालची है कलन विधि एक लालची दृष्टिकोण का उपयोग करके भारित अप्रत्यक्ष ग्राफ पर न्यूनतम फैले हुए पेड़ को खोजने के लिए। के मामले में प्राइम का एल्गोरिदम , हम बार-बार उस शीर्ष का चयन करते हैं जिसकी स्रोत शीर्ष से दूरी कम से कम हो, अर्थात, स्थानीय रूप से वर्तमान इष्टतम पसंद।
इसे ध्यान में रखते हुए, क्या प्राइम के एल्गोरिदम में चक्र हो सकते हैं?
प्राइम का एल्गोरिदम . प्राइम का एल्गोरिदम स्पष्ट रूप से एक फैले हुए पेड़ को बनाता है, क्योंकि नहीं साइकिल कर सकते हैं पेड़ और गैर-पेड़ के कोने के बीच किनारों को जोड़कर पेश किया जा सकता है।
दिए गए ग्राफ प्राइम के एल्गोरिदम या क्रुस्कल के एल्गोरिदम के न्यूनतम फैले हुए पेड़ के निर्माण में कौन सा एल्गोरिदम अधिक कुशल है और क्यों?
क्रुस्कल का एल्गोरिथम अगले सबसे सस्ते किनारे को मौजूदा में जोड़कर सबसे सस्ते किनारे से समाधान विकसित करता है पेड़ / वन। प्राइम का एल्गोरिदम घने के लिए तेज़ है रेखांकन . क्रुस्कल का एल्गोरिथम विरल के लिए तेज है रेखांकन.
सिफारिश की:
काम चालू करने के लिए आप जिन लैंप को छूते हैं, वे कैसे काम करते हैं?

इसका मतलब यह है कि अगर कोई सर्किट लैंप को इलेक्ट्रॉनों से चार्ज करने की कोशिश करता है, तो उसे 'भरने' के लिए एक निश्चित संख्या की आवश्यकता होगी। जब आप दीपक को छूते हैं, तो आपका शरीर अपनी क्षमता में इजाफा करता है। आपको और लैंप को भरने के लिए अधिक इलेक्ट्रॉनों की आवश्यकता होती है, और सर्किट उस अंतर का पता लगाता है
मेरा iPhone 7 एडेप्टर काम क्यों नहीं करता है?

ये अलर्ट कुछ कारणों से प्रकट हो सकते हैं: आपके iOS डिवाइस में एक गंदा या क्षतिग्रस्त चार्जिंग पोर्ट हो सकता है, आपकी चार्जिंग एक्सेसरी ख़राब, क्षतिग्रस्त, या गैर-Apple-प्रमाणित है, या आपका USB चार्जर डिवाइस को चार्ज करने के लिए डिज़ाइन नहीं किया गया है। इन चरणों का पालन करें: अपने डिवाइस के निचले हिस्से में चार्जिंग पोर्ट से कोई भी मलबा हटा दें
आप गैलेक्सी ग्रैंड प्राइम पर कॉल कैसे ब्लॉक करते हैं?
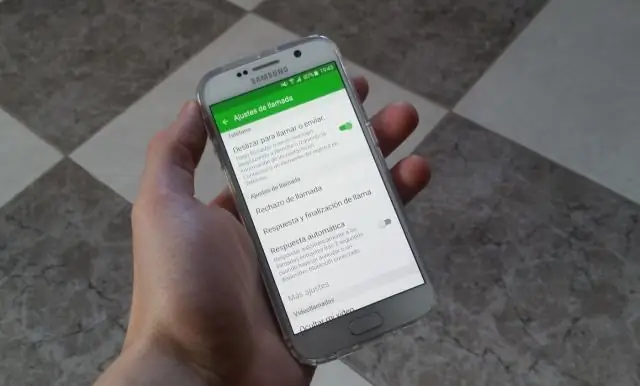
कॉल ब्लॉक करें होम स्क्रीन से, फ़ोन आइकन टैप करें। अधिक टैप करें। सेटिंग्स टैप करें। कॉल अस्वीकृति टैप करें। ऑटो रिजेक्ट लिस्ट पर टैप करें। नंबर को मैन्युअल रूप से दर्ज करने के लिए: नंबर दर्ज करें। यदि वांछित है, तो मिलान मानदंड विकल्प चुनें: संख्या खोजने के लिए: संपर्क आइकन टैप करें। अज्ञात कॉल करने वालों को ब्लॉक करने के लिए, स्लाइड को अज्ञात पर चालू करें
अनुक्रमिक एल्गोरिदम कैसे काम करता है?
कंप्यूटर विज्ञान में, अनुक्रमिक एल्गोरिदम या सीरियल एल्गोरिदम एक एल्गोरिदम है जिसे अनुक्रमिक रूप से निष्पादित किया जाता है - एक बार शुरू से अंत तक, अन्य प्रसंस्करण निष्पादन के बिना - समवर्ती या समानांतर में विपरीत
मुझे एल्गोरिदम और डेटा संरचनाएं क्यों सीखनी चाहिए?

डेटा संरचनाएं और एल्गोरिदम प्रोग्रामिंग में एक महान भूमिका निभाते हैं, लेकिन केवल तभी जब आप वास्तव में जानते हैं कि प्रोग्राम कैसे लिखना है। इन संरचनाओं का अध्ययन करना महत्वपूर्ण है क्योंकि जटिल कंप्यूटिंग समस्याओं जैसे खोज, सॉर्ट, हैशिंग आदि में ऐसी कई संरचनाओं का उपयोग किया जाता है। एल्गोरिदम डेटा को संसाधित करने का तरीका है
